Where is the Math in Spirographs?
In our own teaching practice, we don’t start with presenting the math theory when introducing the Spiro Inquiry activity to students. We find that letting students explore their ideas within the playground of complex math can be a more creative and generative experience. However, having these explanations available when students or educators become curious is always helpful. In this section we offer three explanations that help us understand the math below the surface of spirographs.
Relationships between Gear Numbers
The number of petals a Sprio drawing has has to do with the ratio relationship between the numbers of the teeth in each the inner and the outer gears. When the pen stops making new loops and starts re-tracing what’s already been drawn, this indicates that the inner gear and outer gear have reached the same place that they started. Some gear ratios take more laps before meeting at the point where they started than others. These figures representing the inner and outer gears as if they were flattened out into straight pieces can help visualize this phenomenon:
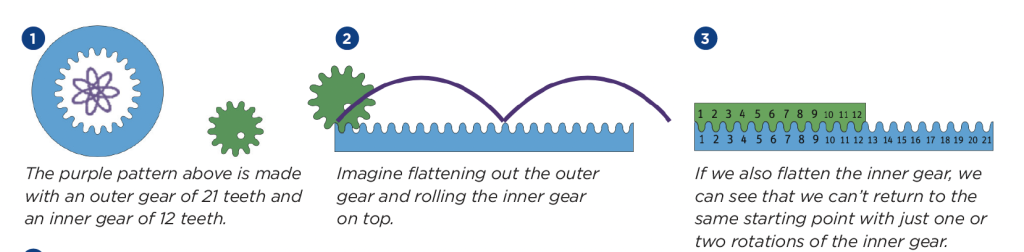


Periodicity in Music
Similar patterns can be found in the rhythms of music. For example, the polyrhythms of sub-Saharan African music interlace different rhythms at once. One drummer might be playing every third beat (red dots), and another musician clapping on the first of every four beats (blue dots), meaning they would only play on the same beat at the same time every four bars. Below is a simplified visualization of just two polyrhythms:
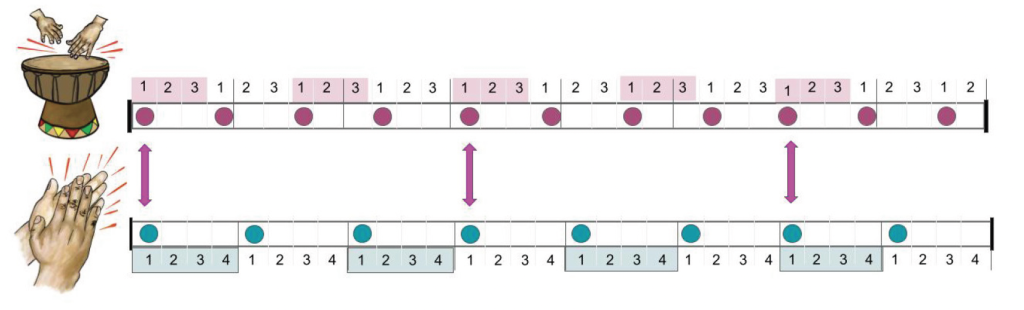
Hypotrochoid Patterns
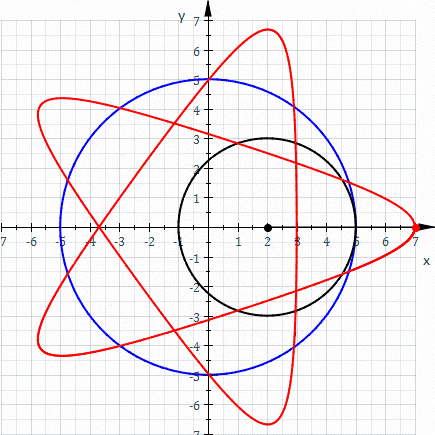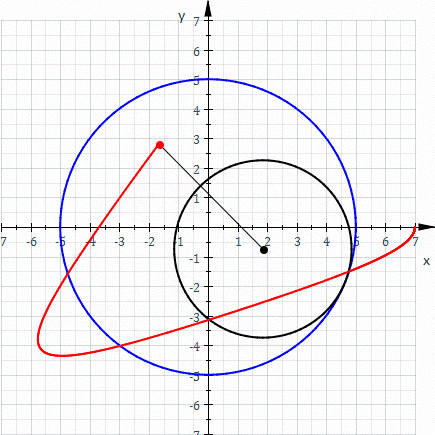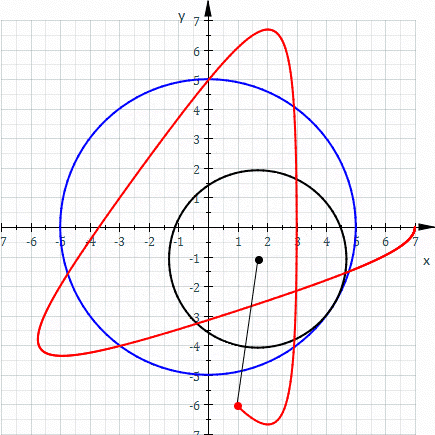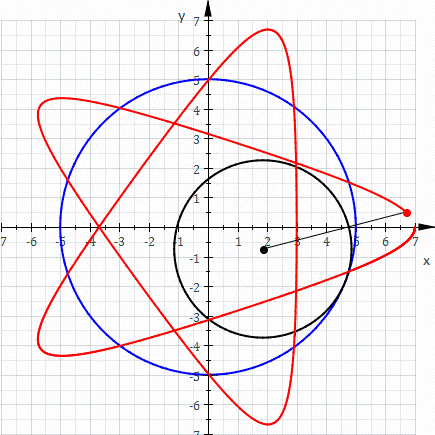
The red curve is a hypotrochoid drawn as the smaller black circle (r) rolls around inside the larger blue circle (R). The distance of the pen from the center of the smaller black circle is represented as d. (parameters are R = 5, r = 3, d = 5). *Image borrowed from here.
One of the underlying math principles represented in the Spiro designs are called Hypotrochoid patterns (shown above). These are algorithmic graphs that Spiro allows young people to play with the mathematics of hypotrochoid graphs without needing to first understand the more abstract equations behind them. By experimenting with the different gear parameters and their resulting designs, honing their own aesthetic motivations, and following their mathematical intuitions, students are developing their own understanding of this graphing concept/phenomena.
IN THEIR OWN WORDS
While hypotrochoid curves and periodicity are not usually on K-12 math curricula, multiplicative and proportional reasoning are. Helping educators and learners see how these concepts are present within everyday, artistic activity is useful for making connections between curriculum and play. Introducing projects that involve complex concepts can reveal that kids are capable of more advanced thinking than we might expect. The Spiro Inquiry makes complex concepts accessible for children without walking them through the simplest ideas first. We encourage facilitators to look for evidence of mathematical sense-making in the everyday language that young people use while playing with Spiro. For example, consider how this exchange between two children demonstrates thinking about the relationships between size, distance, and speed as a very small gear moves around a large one:
Examples from a Diversity of Student Thinking
These examples demonstrate that young people can use the Spiro tool to create a wide variety of designs and ideas. Facilitators can encourage this by explicitly treating Spiro as a process of discovery and creativity rather than coming to predetermined results and conclusions.

