¿Dónde Están Las Matemáticas?
En nuestra propia enseñanza, no comenzamos con la presentación de la teoría matemática cuando presentamos la actividad Spiro a los estudiantes. Descubrimos que permitir que los estudiantes exploren sus ideas dentro del patio de recreo de las matemáticas complejas puede ser una experiencia más creativa y generativa. Sin embargo, es útil tener estas explicaciones disponibles siempre y cuando los estudiantes o educadores sientan curiosidad. En esta sección ofrecemos tres explicaciones que nos ayudan a entender las matemáticas debajo de la superficie de los diseños de Spiro.
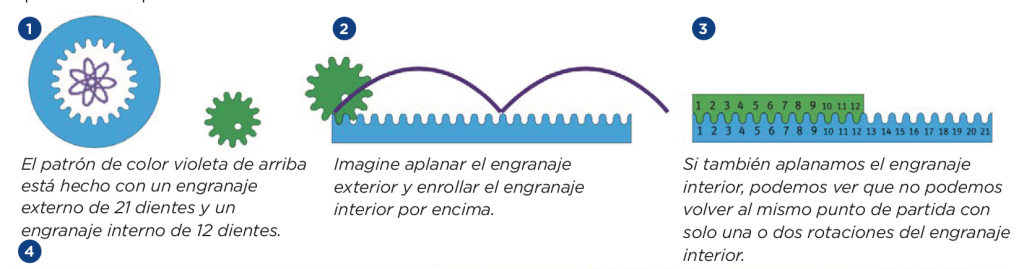
Relaciones entre los números de engranajes
El número de pétalos que tiene un dibujo de Spiro tiene que ver con la relación entre los números de los dientes en los engranajes internos y externos. Cuando la pluma deja de hacer nuevos bucles y comienza a volver a rastrear lo que ya se ha dibujado, el engranaje interno y el engranaje externo han llegado al mismo lugar donde comenzaron. Algunas relaciones de engranajes requieren más vueltas que otras antes de alcanzar el punto en el que comenzaron. Estas figuras representan los engranajes internos y externos como si estuvieran aplanados en piezas rectas:


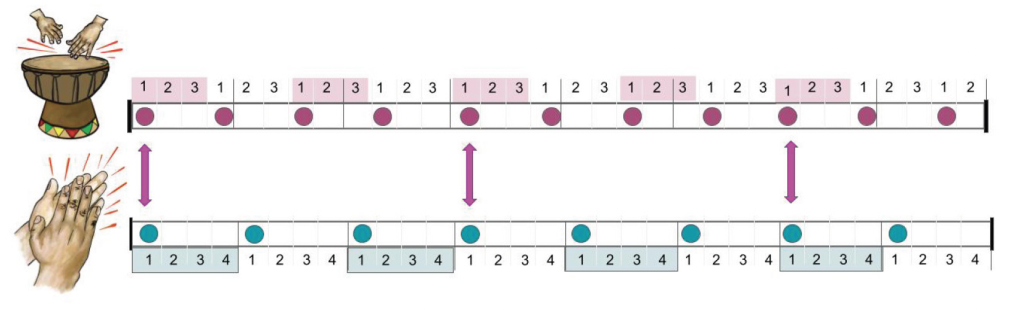
Periodicidad en Música
Patrones similares se pueden encontrar en los ritmos de la música. Por ejemplo, los polirritmos de la música africana subsahariana entrelazan diferentes ritmos a la vez. Un baterista podría estar tocando cada tercer tiempo (puntos rojos), y otro músico aplaudiendo el primero de cada cuatro tiempos (puntos azules), lo que significa que solo tocarían en el mismo tiempo cada cuatro compases. A continuación se muestra una visualización simplificada de solo dos polirritmos:
Patrones Hipotrocoides:
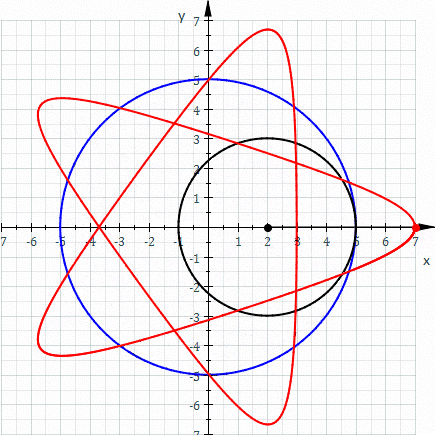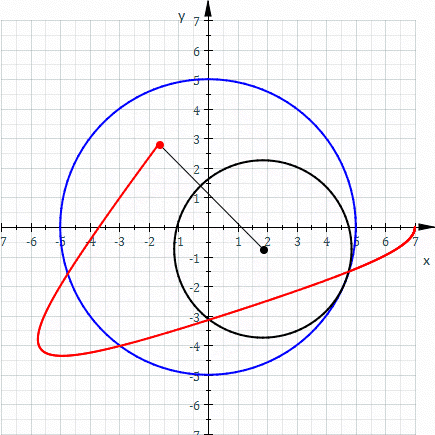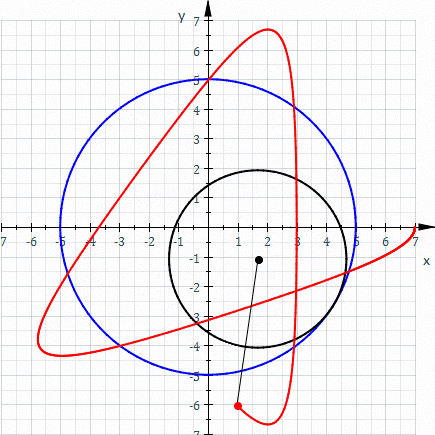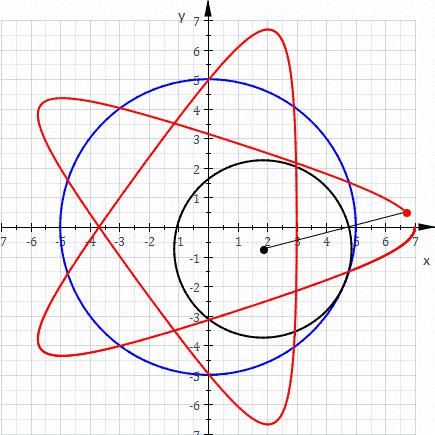
Uno de los principios matemáticos subyacentes representados en los diseños de Spiro se llaman patrones hipotrochoides (mostrados arriba). Spiro permite a los jóvenes jugar con las matemáticas de las gráficas hipotrochoides sin necesidad de entender primero las ecuaciones más abstractas detrás de ellas. Al experimentar con los diferentes parámetros de engranajes y sus diseños resultantes, perfeccionar sus propias motivaciones estéticas y seguir sus intuiciones matemáticas, los estudiantes están desarrollando su propia comprensión de este concepto/fenómeno gráfico.
La curva roja es un hipotrochoide dibujado como el círculo negro más pequeño (r) rueda dentro del círculo azul más grande (R). La distancia de la pluma desde el centro del círculo negro más pequeño se representa como d. (Los parámetros son R = 5, r = 3, d = 5). *Imagen prestada de wikipedia
EN SUS PROPRIAS PALABRAS
Mientras que las curvas hipotrocoides y la periodicidad no suelen estar en los planes de estudio de matemáticas K-12, el razonamiento multiplicativo y proporcional sí lo están. Ayudar a los educadores y estudiantes a ver cómo estos conceptos están presentes en la actividad artística cotidiana es útil para establecer conexiones entre el plan de estudios y el juego. La introducción de proyectos que involucran conceptos complejos puede revelar que los niños son capaces de pensar de manera más avanzada de lo que podríamos esperar. Las Investigaciones Spiro hace que los conceptos complejos sean accesibles para los niños sin guiarlos a través de las ideas más simples primero. Animamos a los facilitadores a buscar evidencia de sentido en el lenguaje cotidiano que los jóvenes usan mientras juegan con Spiro. Por ejemplo, considere cómo este intercambio entre dos niños demuestra sus pensamientos en las relaciones entre el tamaño, la distancia y la velocidad a medida que un engranaje muy pequeño se mueve alrededor de uno grande:
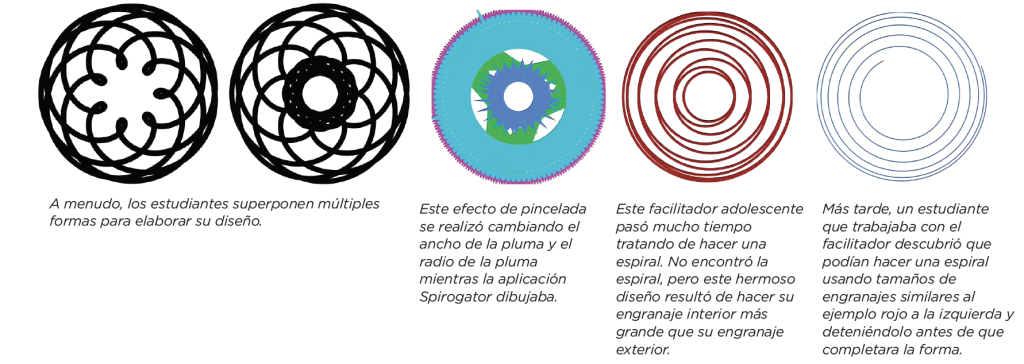
EJEMPLOS DE UNA DIVERSIDAD DE PENSAMIENTO
Estos ejemplos demuestran que los jóvenes pueden utilizar la herramienta Spiro para crear una amplia variedad de diseños e ideas. Los facilitadores pueden fomentar esto tratando explícitamente a Spiro como un proceso de descubrimiento y creatividad en lugar de llegar a resultados y conclusiones predeterminados.